まずは、デスクトップ上のアイコンをダブルクリックします。 (これですね。→
すると次のような画面が開きます。
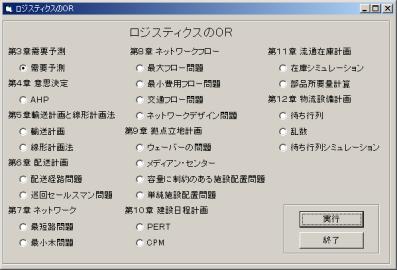
今回は、線形計画問題を解くので、第5章の中の“線形計画法”を選び実行します。
(白い丸のところをマウスでクリックすると、中に黒い点がつきますので、その後“実行”ボタンをクリックしてください。)
線形計画法の画面が開きます。
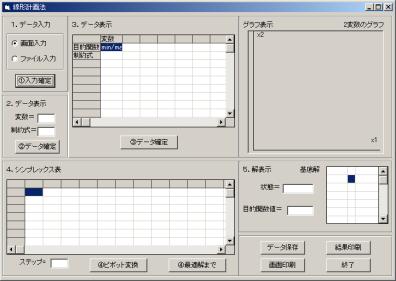
線形計画問題
メディアステーションのPCにインストールされているORのソフトウェアを用いた線形計画問題の解き方をご紹介します。
まずは、デスクトップ上のアイコンをダブルクリックします。 (これですね。→![]() )
)
すると次のような画面が開きます。

今回は、線形計画問題を解くので、第5章の中の“線形計画法”を選び実行します。
(白い丸のところをマウスでクリックすると、中に黒い点がつきますので、その後“実行”ボタンをクリックしてください。)
線形計画法の画面が開きます。

以後、画面上の番号に従って作業を進めていきます。
※この先は画像を載せずに説明しますから、できればソフトの方も立ち上げてそちらと照らし合わせながら手順を追ってください。
1.“データ入力”方法を決める。
データの入力方法には画面入力とファイル入力がありますが、今回は簡単な画面入力の方を使います。黒い点が画面入力の方についていることを確認して“①入力確定”のボタンをクリックします。
2.“データ表示”を決める。
解きたい問題の情報を入力します。目的関数の中に含まれている変数(決定変数)の数を“変数=”の後ろの白いボックスに入力します。また、制約式の数を“制約式=”の後ろの白いボックスに入力します。両方入力したら、“②データ確定”のボタンをクリックします。
3.“データ表示”をする。
<目的関数の入力>
1行1列目のセルに“min/max”とあり、そこがアクティブに(青く)なっています。ここは、解きたい問題が最大化問題なら“max”、最小化問題なら“min”と入力します。(セルをダブルクリックすると“min/max”の表示が消えますので、その後改めてタイプしてください。)
1行2列目のセル(x1のすぐ下のセル)には、目的関数の変数x1の係数を、1行3列目のセル(x2のすぐ下のセル)のは、目的関数の変数x2の係数を入力します。
<制約式の入力>
2行2列目のセルに、第1番目の制約式の変数x1の係数を入力します。2行3列目のセルに、第1番目の制約式の変数x2の係数を入力します。2行4列目のセルには不等号を入力しますが、「≦」は半角の「<」、「≧」は半角の「>」、「=」は半角の「=」を入力してください。2行5列目のセルには、制約式の右辺の定数を入力します。
制約式は、以上のようなやり方で2行目以降に必要な数だけ入力してください。
目的関数とすべての制約式を入力したら、“③データ確定”のボタンをクリックします。
4.“シンプレックス表”が表示される。
手順3で“③データ確定”のボタンをクリックすると、初期基底解によるシンプレックス表が表示されます。それと同時に、変数が2つの場合は、グラフ表示のところにグラフが表示されます。(変数が3つ以上のときは、グラフは表示されません。)
5.“解表示”がされる。
<最適解を求める>
手計算でやるときと同様に、1段ずつ作業を進めて行きたいならば、“④ピボット変換”のボタンをクリックしてください。そうすると、シンプレックス表の数値が変化します。2変数の時なら、基底解に対応した端点(青い点)がグラフ上を移動します。もう一度“④ピボット変換”のボタンをクリックしてください。表の数値が変わって、解(青い点)が次の端点に移動します。“④ピボット変換”のボタンをクリックしても、表の数値が変わらず、青い点も移動しなくなったら、最適解に到達したということです。(5.解表示のところにある“状態=”の横のボックスの表示が“基底解”から“最適解”に変わります。)そこで終了です。
一気に最適解を出したいときは、“④最適解まで”というボタンをクリックしてください。それで、最適解が表示されます。
<解の表示>
“状態=”の横のボックスに“最適解”と表示されていることを確認します。“目的関数値=”の横のボックスに表示されている数値が最適な目的関数の値です。また、“基底解”の横に表示されているx1、x2、・・・、xnが、目的関数を最適にする変数の値です。その下に表示されるλの値は、制約式のゆとりをあらわしています。
例題
次の線形計画問題を解いた答えの画面だけ載せておきます。見にくいですけど、参考にしてください。
問題 3種類の原料(A,B,C)を使って、2種類の製品(Ⅰ,Ⅱ)を生産します。各製品を1単位生産するのに必要な原料量とその月間使用制限量は以下の表にあるとおりです。また、製品Ⅰの1単位当たりの利益は9、製品Ⅱの1単位当たりの利益は7となっています。このとき、総利益を最大とする生産計画を立ててください。
表)各製品を1単位生産するのに必要な原料量とその月間使用制限量
| 製品Ⅰ | 製品Ⅱ | 月間使用制限量 | |
| 原料A 原料B 原料C |
15 5 4 |
6 10 18 |
900 500 720 |
解き方 まず、製品Ⅰの生産量を x1, 製品Ⅱの生産量を x2 , 総利益を Z としてこの問題を線形計画の表現で定式化します。
max Z= 9 x1 + 7 x2
s.t. 15 x1 + 6 x2≦ 900
5 x1 + 10 x2≦ 500
4 x1 + 18 x2≦ 720
x1≧ 0 x2≧ 0
次に、ORのソフトを使ってこの最大化問題を解きます。
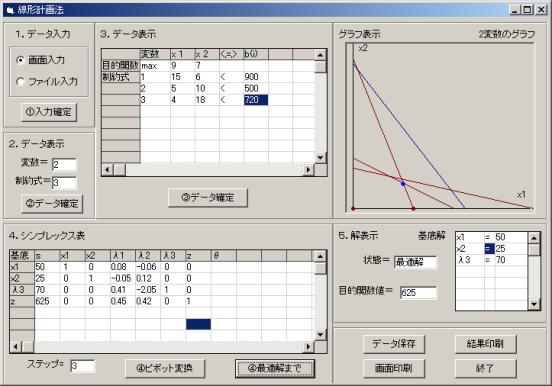 解の読み方
解の読み方
総利益を最大にする 生産計画は製品Ⅰを50単位、製品Ⅱを25単位生産するという計画であり、その時の総利益は625です。
(また、λ3=70 より原料Cは、月間使用制限量に70単位の余裕があることがわかります。その他の原料は、全て使い切っています。)
(こんな説明で分かっていただけたかなぁ。(^^;))